বড় সংখ্যার আইন

বড় সংখ্যার আইন কি?

আর্থিক দৃষ্টিকোণ থেকে, বৃহৎ সংখ্যার আইনটি পরামর্শ দেয় যে বৃহৎ সংস্থা যেটি দ্রুত বৃদ্ধি এবং বিকাশের সম্মুখীন হয়েছে তা চিরকাল মহাকাশের গতিতে বাড়তে পারে না। এটি প্রায়শই শতাংশে গণনা করা হয়। এটি বলে যে ব্যবসার বৃদ্ধির গতি চিরকাল একই থাকার সম্ভাবনা খুব কম। বৃহৎ সংখ্যার উত্সের আইনটি 16 শতকে তৈরি হয়েছিল। "জেরোলামা কার্ডানো" নামে একজন বিখ্যাত গণিতবিদ এই আইনটি চিহ্নিত করেছিলেন। যদিও তিনি তা প্রমাণ করতে পারেননি। অবশেষে, জ্যাকব বার্নোলি 1713 সালে এই আইনটি প্রমাণ করেছিলেন।

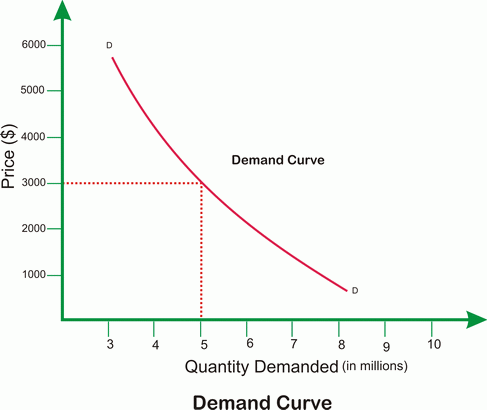
বড় সংখ্যার আইনটি সাধারণত পরিসংখ্যানে ব্যবহৃত হয়। আসলে আইনটি বিভিন্ন বিষয়ে প্রযোজ্য। প্রয়োজনীয় তথ্য সংগ্রহের জন্য প্রদত্ত জনসংখ্যা থেকে প্রতিটি ব্যক্তির জরিপ করা কার্যত সম্ভব নয়। যাইহোক, এটি পরামর্শ দেয় যে আপনি যত বেশি লোক জরিপ করবেন, আপনার ফলাফল সঠিক বা গড়ের কাছাকাছি হওয়ার সম্ভাবনা তত বেশি। চলুন ব্যবসা এবং পরিসংখ্যান পরিপ্রেক্ষিতে বৃহৎ সংখ্যার আইনের প্রয়োগ বোঝা যাক।

বড় সংখ্যা এবং ব্যবসা বৃদ্ধির আইন

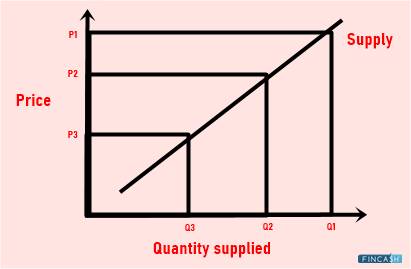
ব্যবসা এবং আর্থিক শিল্পে, বড় সংখ্যার আইন কোম্পানির বৃদ্ধি চক্র নির্দেশ করে। উপরে উল্লিখিত হিসাবে, এটি পরামর্শ দেয় যে সংস্থাটি সব সময় একই হারে বিকাশ করতে পারে না। যাইহোক, এই পর্যবেক্ষণ বড় সংখ্যার আইন থেকে নয়। এটি বরং প্রান্তিক আয় হ্রাস করার আইন থেকে উদ্ভূত।

উদাহরণ স্বরূপ, ওয়ালমার্ট ইনকর্পোরেটেড 2015 সালে $485.5 বিলিয়ন আয়ের রিপোর্ট করেছে। একই বছরে, Amazon $95.8 বিলিয়ন আয়ের রিপোর্ট করেছে। যদি Walmart Inc এর বৃদ্ধি করার সিদ্ধান্ত নেয়আয় 50% দ্বারা, এটি একটি অতিরিক্ত $242 বিলিয়ন করতে হয়েছে. অন্যদিকে, একই লক্ষ্য অর্জনের জন্য অ্যামাজনের প্রয়োজন হবে মাত্র 47.9 বিলিয়ন ডলার। এখন, বৃহৎ সংখ্যার আইন পরামর্শ দেয় যে ওয়ালমার্টের জন্য অ্যামাজনের তুলনায় 50% বৃদ্ধি করা আরও চ্যালেঞ্জিং হবে।

পরিসংখ্যানে বড় সংখ্যার আইন

পরিসংখ্যানে, বৃহৎ সংখ্যার আইনকে একটি উপপাদ্য হিসাবে সংজ্ঞায়িত করা যেতে পারে যা একাধিকবার একটি পরীক্ষা করার ফলাফলকে বলে। আইনটি পরামর্শ দেয় যে বিপুল সংখ্যক পরীক্ষা থেকে উৎপন্ন ফলাফল প্রত্যাশিত মানের কাছাকাছি হতে পারে। তা ছাড়া, আরও পরীক্ষা-নিরীক্ষা সঞ্চালিত হওয়ায় এটি গড়ের কাছাকাছি যাওয়ার সম্ভাবনা রয়েছে। উপপাদ্যটি পরিসংখ্যানে অত্যন্ত গুরুত্বপূর্ণ কারণ এটি একটি স্থিতিশীল দীর্ঘমেয়াদী ফলাফল প্রদান করে।

একটি উদাহরণ দিয়ে বিষয়টি বোঝা যাক। ধরুন আপনি একটি ক্যাসিনোতে রুলেটের চাকা ঘোরান। আপনি রাউন্ড জিতুন. ক্যাসিনো অবশ্যই একটি স্পিন হারিয়েছে, কিন্তু আপনি যদি প্রচুর সংখ্যক স্পিন সঞ্চালন করেন, ফলাফল ক্যাসিনোর পক্ষে হতে পারে। অন্য কথায়, প্রতিটি স্পিন দিয়ে ক্যাসিনো তার প্রত্যাশিত বা অনুমানযোগ্য মানের কাছাকাছি পৌঁছানোর একটি ভাল সুযোগ রয়েছে।

এখানে উল্লেখ্য একটি গুরুত্বপূর্ণ বিষয় হল যে বৃহৎ সংখ্যার আইনটি ফলাফলের ক্ষেত্রে প্রযোজ্য যেখানে বিপুল সংখ্যক পরীক্ষা বা পরীক্ষা করা হচ্ছে।