Harmonic Mean

What is Harmonic Mean?

In order to calculate the harmonic mean of the given figures, you are supposed to divide the total number of observations by each number’s reciprocal. Let’s understand harmonic mean definition with an example.

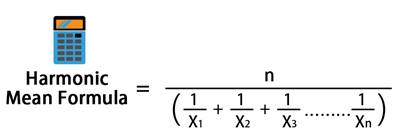
Suppose you are asked to calculate the harmonic mean of 1, 3, 5, and 10. Now that you have a total of 4 observations, you will be dividing 4 by the sum of each number’s reciprocal, i.e. 1/1 + 1/3 + 1/5 + 1/10. On dividing the total you get from the sum of these reciprocals by 4, you will get the harmonic mean of this calculation.

An overview of the Harmonic Mean

Also known as the subcontrary mean, the harmonic mean is considered as a common calculation option for calculating the average of the given figures. It is important to note that harmonic mean happens to be concave. With that being said, you need to pay special attention to the numbers you use for calculating the average. Here, you cannot use negative numbers.

Harmonic mean is a part of the Pythagorean mean, which consists of a total of three means (the first and the second one being the arithmetic mean and the geometric mean respectively). The harmonic mean will be the same as arithmetic and geometric mean if the given values are the same.

For example, all three Pythagorean means will be 4 if the given values are 4, 4, and 4. Since arithmetic mean is quite commonly used, the harmonic mean is often confused with the arithmetic mean. In many places, harmonic means give the best possible average. Note that harmonic mean is mainly used for the calculation of the average when the given value is expressed in ratios and rates.

We are going to take another example to understand where the arithmetic and harmonic means are calculated.

Harmonic Mean Vs Arithmetic Mean

Take, the speed of the vehicle and its distance, for example. Let’s say a train has covered a specific distance traveling at a particular speed. Now, if it covers the same distance when returning, then the average speed of the train will be calculated using the harmonic mean. This mathematical formula will help you find the average speed at which the train must have returned to the destination. If this train travels at different speeds yet take equal time to reach the destination, then you are going to need to calculate the arithmetic mean to get the average speed of the train.

The same example applies to every calculation, in which the user tries to figure out the average speed of the vehicle given the distance traveled. If your vehicle covers the same distance at different speeds, then you need to use harmonic mean to calculate the average speed of the vehicle.