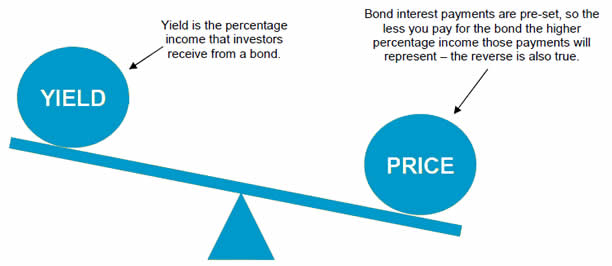
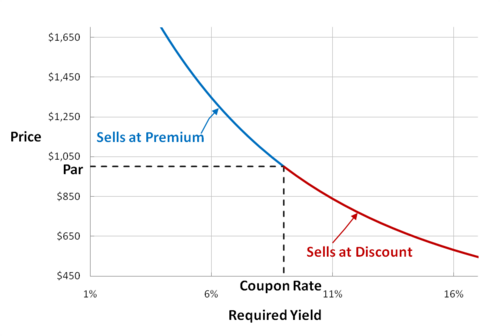
What is Effective Yield?

Effective yield is defined as a yearly rate of return at a periodic rate of interest on Bonds. The other name for it is Annual Percentage Yield (APY). It is regarded as one of the most accurate measures of an equity holder's return because, unlike the nominal yield method, it takes compounding into account.

It is also based on the assumption that an equity holder is eligible to reinvest their coupon payments at a coupon rate.

More About Effective Yield

To calculate the effective yield, you need to know how much your bond's coupon rate is in the percentage of its Face Value. It is common for bond issuers to send coupon payments to bondholders on a biannual Basis. That's two coupon payments every year for the investor to look forward to. In order to compute the effective yield, divide the coupon payments by the bond's current Market value. Bondholders can assess their yields on bonds in different ways. In addition to effective yield, there's the current yield, which measures a bond's yearly return based on its annual coupon payments and current price rather than its face value.

Given that interest rates fluctuate owing to many economic variables, this is not always viable; coupon payments cannot be reinvested in another product with the same interest rate. This is the major downside of effective yield; it assumes the opposite thing.

Effective Yield Formula

Learn how you can calculate the effective yield on the bond with the help of a simple mathematical formulation.

Effective Yield = [1 + (i/n)]n – 1

In this formula,

• ‘i’ represents the nominal rate of interest
• ‘n’ represents the number of payments received yearly

For Example - Company XYZ issues an 8% coupon bond, and you decide to purchase it. The nominal interest rate is 8%. Find out what the effective yield is if the interest is paid every year?

The nominal rate of interest is 8%, and it’s given the interest is paid yearly, which means the number of payments equals 1. According to the formula, the yield on the 8% coupon bond is calculated as follows:

i = (1+[8%/1]^1-1

i = 8%

Why Effective Yield?

When comparing alternative investment options, when interest rates are stated at varying compounding rates, the effective yield seems to be quite helpful. Once all of the rates have been converted into effective yearly returns, you can then take a well-suited decision. Let’s take an example; you have the option to choose between two bonds, A and B, with nominal interest rates of 5% compounded semi-annually and 4.9% compounded monthly, respectively.

In light of the differing compounding periods, a direct comparison is impossible. In this scenario, effective yield works wonders. You can compute the effective yearly yields for each bond. The effective yield for A equals 5.0625%, and that of B equals 5.0848%. Clearly, option B is a better investment opportunity as the returns are higher than A.

Effective Yield and Bond Equivalent Yield

Measurement of the investment return obtained by the coupon payments received from a bond is called the effective yield, whereas the equivalent bond yield is a measure of investment return based only on the face value (par value) of the bond. It is paid out to the bondholder when the bond matures, as well as the price at which it was acquired.

This means that coupon payments are not included in the bond equivalent yield calculation. When calculating the investment return on a zero-coupon bond, which does not give coupon payments other than the interest received when the bond reaches maturity and is redeemed by the issuer, this formula is used to determine the bond equivalent yield.