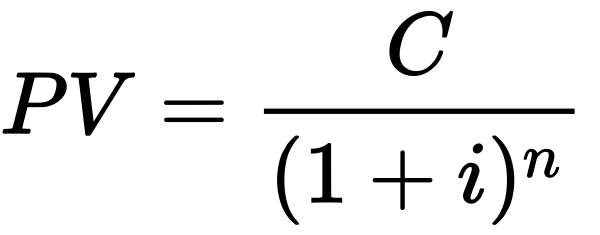What is Net Present Value?

The present value of all future cash flows, both positive and negative, discounted over the whole life of an investment is known as Net Present Value (NPV). It is widely used in finance and Accounting valuation to determine the actual worth of factors.

These factors include business, investment security, Capital project, new venture, cost-cutting programme, and other cash-flow-related items.

Net Present Value Method

The Net Present Value method is a financial analysis technique for determining the viability of an investment in a project or a business. When compared to the initial investments, it is the present value of future cash flows.

Net Present Value Calculation

The gap between the present value of cash inflows and the present value of cash withdrawals over a period of time is defined as NPV. The mathematical formula is:

NPV = {Net cash flow/ (1+I)^T }

Where,

• I = Interest rate
• T = Time period

Net Present Value Example

Consider an Rs. 1,000 projects that will generate three cash flows of Rs. 500, Rs. 300, and Rs. 800 over the following three years.

Assume the project has no Salvage Value and the needed rate of return is 8%.

The following formula is used to determine the project's net present value:

• NPV = [500/(1+0.08)^1 + 300/(1+0.08)^2 + 800/(1+0.08)^3 ] - 1000
• NPV = [462.96+257.20+640] - 1000
• NPV = 1360.16 - 1000
• NPV = 360.16

Net Present Value vs Present Value

Given a predetermined rate of return, Present Value (PV) is the current value of a future quantity of money or cash flow stream.

Meanwhile, the difference between the present value of cash inflows and outflows over time is known as NPV.

Net Present Value Formula in Excel

The XNPV function in Excel can be used to determine the NPV. Unlike the NPV function, which assumes that all time periods are equal, XNPV considers the precise dates of each cash flow. Since cash flows are typically generated at irregular periods, XNPV is a more realistic estimate of NPV.

The XNPV Excel formula is as follows:

=XNPV (Rate, Values, Dates)

Where,

• Rate: The appropriate discount rate depending on the cash flows' riskiness and potential returns
• Values: An array of cash flows that includes all cash outflows and inflows
• Dates: These are the dates for the cash flow series that were chosen in the "values" array

Importance of Net Present Value

NPV helps estimate the worth of a project, an investment, or any set of cash flows. It is a comprehensive statistic considering all Income, expenditures, and capital costs related to a given investment.

In addition to all income and expenditures, it considers the period of each cash flow, which can substantially impact the present value of an investment. On the contrary, it's better to pay attention to cash inflows first and outflows afterwards.

Positive Vs. Negative Net Present Value

Positive Net Present Value

It implies that a project's or investment's estimated profits surpass its anticipated expenses. An investment that results in a positive net present value is profitable.

Negative Net Present Value

A negative NPV investment will result in a net loss. This principle underpins the rule that only investments with positive NPV values should be computed.

Here are the generalised rules of the NPV method to keep in mind:

• If the NPV is greater than zero, it is an acceptable situation (Profitable)
• If the NPV is zero, the situation is indifferent (Break-Even Point)
• If the NPV is less than zero, reject the proposal (Unprofitable)

Net Present Value Advantages and Disadvantages

Advantages

NPV of a possible investment opportunity is a financial statistic that attempts to represent the overall worth of the opportunity. Here is the list of pros:

• NPV analysis uses the temporal value of money, which converts future cash flows into the worth of today's rupees
• Since purchasing power is undermined by Inflation, NPV is a far more relevant estimate of your project's prospective profitability
• The formula gives a single, unambiguous number that the manager can compare against the initial investment to determine the project or investment's performance

Disadvantages

NPV is the most widely applied approach for analysing investment prospects; it has certain disadvantages that should be considered. The following are some of the major barriers to NPV analysis:

• Difficult to make accurate risk adjustments
• Data manipulation is easier
• Assumption of the discount rate being constant overtime period
• Sensitive to small changes in assumption
• Comparison of projects of different sizes is not possible

Conclusion

Net present value reduces a project's necessary investment by discounting all future cash flows. Most software nowadays does NPV calculations and assists managers in making decisions.

Despite its drawbacks, this technique is commonly used in capital budgeting. The Net Present Value of a possible investment opportunity is a financial metric that attempts to represent the overall potential of the opportunity.